Tibor bá’ online
 Prológus: Hívőknek ajánlom, hogy alaposan rágják át magukat az anyagon, mert itt kőrvonlazódik a valós fizikai világ és az anyagmentes „más világ” közötti határvonal.
Prológus: Hívőknek ajánlom, hogy alaposan rágják át magukat az anyagon, mert itt kőrvonlazódik a valós fizikai világ és az anyagmentes „más világ” közötti határvonal.
Az elképzelés, miszerint a megfigyelő jelenléte megváltoztatja a kvantumvilág viselkedését, már közel nyolcvan éve izgatja a kutatókat. Ennek most vége, mondja Yakir Aharonov a Tel Avivi Egyetem fizikusa, aki egyben a Dél-Karoliniai Egyetem munkatársa is. Már jó ideje tudjuk, hogy a szubatomi részecskék titokzatosan viselkednek. Példának okáért egyetlen elektron egy azon időben „perdülhet” jobbra is és balra is, vagy pedig szimultán létezhet két különböző helyen. Az pedig egyenesen kvantummechanikai tantétel, miszerint abban a pillanatban, amikor valaki meg akar figyelni egy szuperpozíciót (például a fent említettek egyikét), a megfigyelni kívánt részecske azonnal „normális” viselkedésbe kezd. Ez az oka annak, hogy Schrödinger híres macskája csak addig maradhat egyszerre élő is meg holt is, amíg valaki bele nem néz dobozába. Amint kinyitjuk a doboz fedelét a macska vagy él, vagy ki van múlva. Így aztán ez a titokzatos világ kifürkészhetetlen maradt mind a mai napig, de ennek vége.
csak addig maradhat egyszerre élő is meg holt is, amíg valaki bele nem néz dobozába. Amint kinyitjuk a doboz fedelét a macska vagy él, vagy ki van múlva. Így aztán ez a titokzatos világ kifürkészhetetlen maradt mind a mai napig, de ennek vége.
Aharonov szentül hiszi megtalálta módját, hogyan figyelje meg a kvantumvilágot a szuperpozíció szétrombolása nélkül. A bejelentés természetesen lélegzetelállító és nyolcvan év tanításának az arculcsapása. Aharonov azonban kitart állítása mellett vagy is, hogy az általa kidolgozott „alig-mérés” szétrombolás nélkül képes megmutatni egy adott kvantumállapotot. Múlt évben publikálta tizenöt év munkájának összefoglaló eredményét, ami szerint az alig-mérés segítségével a kvantummechanika korábban megmagyarázhatatlan ellentmondásai új megvilágítást kapnak. A szerző szerint munkájának eredménye „szokatlan és meglepő”, de bizonyítja, hogy a kvantumelmélet logikus és következetes. Éppen ezért az alig-mérés segítségével a kvantumelmélet titokzatos világa megnyitható.
Kezdjük az Oxfordi Egyetemen dolgozó Lucien Hardy 1992-ben kidolgozott paradoxonjával, ami (Schrödinger macskájáéhoz hasonlóan) szintén egy gondolat kísérlet eredménye. Hardy az mutatta ki, hogy az anyag és antianyag között nem léphet fel kölcsönhatás. A gondolat kísérletben két Mach-Zender féle interferométer szerepel, vagyis olyan berendezések, melyekben félig áteresztő tükrök vannak beállítva tetszőlegesen kiválasztható szubatomi részecskék útjába. A jól ismert eredmény szerint egy interferométerben szuperpozíciós állapot áll elő, mivel (például) egy foton vissza is verődik a tükörről és át is halad rajta, vagyis egyetlen foton útja kettéválik. Később az interferométerben ez a két útirány egyesül, de hogy ezt követően mi történik az a korábbi eseménytől függ.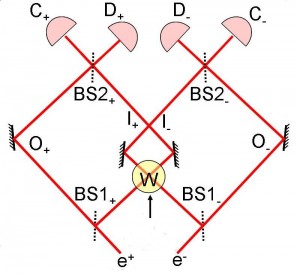 Ugyanis az interferométer útirányaiban található egy másik félig áteresztő tükör, ami úgy van elrendezve, hogy ha a foton zavartalanul haladhatott végig pályáján, vagyis nem találkozott másik részecskével vagy térrel, akkor a „C” jelzésű detektorba érkezett. Ha azonban a fotont haladása közben valami megzavarta asz interferométerben, akkor egy másik „D” jelzésű detektorba érkezhetett.
Ugyanis az interferométer útirányaiban található egy másik félig áteresztő tükör, ami úgy van elrendezve, hogy ha a foton zavartalanul haladhatott végig pályáján, vagyis nem találkozott másik részecskével vagy térrel, akkor a „C” jelzésű detektorba érkezett. Ha azonban a fotont haladása közben valami megzavarta asz interferométerben, akkor egy másik „D” jelzésű detektorba érkezhetett.
Hardy két ilyen interferométert (gondolatban) úgy helyezett el, hogy az egyiknek egy útszakasza egybe essen a másik interferométer egy útszakaszával (lásd az ábrát). Ezt követve a gondolat kísérlet szerint át kell ereszteni egy pozitront (az elektron antirészecskéjét) az egyik interferométeren, és evvel egy időben egy elektront is a másik interferométerben. A két részecskének találkozni kell a két interferométer közös útszakaszában és kölcsönösen meg kell egymást semmisíteni (anihiláció).
Hardy azonban kimutatta, hogy valami sokkal különösebb dolog történik. Ritka körülmények között a kvantumelmélet előrejelzése szerint mind a két „D” detektor egyszerre jelezhet. Valami okból kifolyólag mind a részecske mind pedig az ellen részecskével történt valami, vagyis a D detektor felé tart és mégsem anihilálódnak a közös útszakaszban.
Ez a helyzet azért állhat elő, mert a kvantumelmélet a részecskék többszörös létéből kinyert valószínűségekkel dolgozik. Tekintettel arra, hogy a részecskék egy azon időben (szimultán) lehetnek is és nem is a közös útszakaszban, a kvantumelmélet valószínűsége megenged egy valószínűtlen, de lehetséges olyan eredményt, ami lehetetlen. Ez lenne Hardy paradoxonja.
Az elmúlt évtizedben néhányan „megoldották” Hardy paradoxonját azzal, hogy kijelentették, egy gondolatkísérlet eredménye nem azonos egy valóságos kísérlet eredményével, ezért aztán Hardy elképzelése értelmetlen. A tényleges eseményt az útszakasz megmérésével lehet csak érzékelni a végső eredményből történő egyszerűen visszakövetkeztetés helyett. Viszont, amint elhelyeznek egy részecske érzékelőt az útszakasz bármely részében, a kvantumelmélet szerint a részecske beavatkozást szenved el és így a D detektor garantáltan jelezni fog. Következésképpen a részecske helyzetét nem lehet kikövetkeztetni és evvel a paradoxon elvész.
Sandu Popescu a Bristoli Egyetem és a Bristoli Hewlett-Packard Laboratórium munkatársa azt állítja: az általános felfogás szerint mivel mérés hatására a paradoxon eltűnik, az egész csak figyelem elterelésre jó, nem érdemes rá szót fecsérelni. Viszont Aharonov segítői: a Tel Avivi Egyetemen dolgozó Benni Rezni, a Texasi A&M Egyetem munkatársa Alonso Botero és a Bostoni Egyetemről Jeff Tollaksen kidolgozták Hardy gondolat kísérletének egy módosított változatát, amit laboratóriumban végre lehet hajtani. Számításaik szerint a paradoxon fennmarad, de mivel a kísérlet ténylegesen elvégezhető, a paradoxont nem lehet lesöpörni az asztalról avval, hogy mindössze elvont következtetés, annak a kvantumelmélet objektív igazságának kell lennie.
Az általuk javasolt alig-mérés kihasználja a kvantumbizonytalanságot, vagyis azt a tényt, hogy egy kvantumrendszerben mindig kell lenni belső bizonytalanságnak egy részecske helyzetét és energiáját illetően. Aharonov kvantum detektora oly csekély mértékben kapcsolódik a kísérlethez, hogy a bizonytalansági szint alatti mérést is érzékel. Ezért aztán a detektor hatása van a kísérletre érzékelhetetlen. Elképesztő módon ez azt jelenti, hogy a szuperpozíció megmarad.
Ennek az érzékelésnek azonban meg van az ára, vagyis elképesztően pontatlan, ami az egész eljárást használhatatlanná tehetné, de Aharonov számításai szerint többszöri mérés átlagolásából származó eredmény közel áll a tényleges értékhez.
Képzeljünk el egy elektron mérésére alkalmas mérleg rendszert. Alig-mérés esetében a kvantumbizonytalanság szerint a mérési érték kis mértékben bizonytalan lesz, de ez a kis érték nagyobb lesz mint az elektron súlya. Ennek alapján az elektron súlyát nem lehet megadni. Ha azonban sok milliárd elektront, egymást követve megmérünk, a mérési eredmények átlaga meg fogja adni a tényleges súlyt.
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
Jól értem, hogy Aharonov, Hardy ötletét követve, 2 db Mach-Zender féle interferométert használna?
Hát kissé off, de kreativitásban hasonló:
Számítógépes szimulációban élünk?
http://www.sg.hu/cikkek/94019/szamitogepes_szimulacioban_elunk
„Sandu Popescu a Bristoli Egyetem és a Bristoli Hewlett-Packard Laboratórium munkatársa azt állítja: az általános felfogás szerint mivel mérés hatására a paradoxon eltűnik, az egész csak figyelem elterelésre jó, nem érdemes rá szót fecsérelni. ”
Első olvasatra nekem is ez jutott eszembe ..
2!
Pontosan ez az álmom hogy a gyerekem egy ilyen projektben részt vegyen mesterséges intelligencia programozóként..
Inogni látszik az elektromágnesesség elmélete
http://www.sg.hu/cikkek/93787/inogni_latszik_az_elektromagnesesseg_elmelete
Jó hallani egy fizikustól, hogy „a jövő befolyásolja a jelent”.
De hogy is? Hiszen a jövő még nem létezik, nem? Mint ahogy a múlt sem már. Vagy mégsem így van?
De igazán mindegy is, mert mire kitalálják addigra már 10-es szintű mágussá meditálom magam 😀
https://beleagueredapprentice.files.wordpress.com/2011/08/science-2011-cho-690-3-weak-measurement.pdf
http://discovermagazine.com/2010/apr/01-back-from-the-future
4:
A jó szándékodat nem vonom kétsége, de amit belinkeltél nem sokat ér, sőt azokat alaposan félrevezeti, akik nem ismerik ezt a diszciplínát. Az elektromágnesesség elmélete köszöni szépen jól van, esze ágában sincs inogni. Hogy a gerjesztett atomok fényt bocsátanak ki az nagyon régi dolog. Ezen az elven működtek a régi neoncsövek, majd a fénycsövek, higanygőzlámpák, nátriumgőz lámpák, és újabban a kompakt fénycsövek. A különböző elemek, különböző elektron pályájának energia különbsége szabja meg a foton hullámhosszát, tehát a színét. Ezért használnak különböző fényporokat (ritka földfémek, stb.) az optimális színhőmérséklet eléréséhez. higanygőz és nátriumgőz lámpákra ez nem érvényes, mert ott a Hg és Na atomok gerjednek, és adják le az ismert kék, illetve narancssárga színt. Itt a kísérletnél az történt, hogy a vas atomokat megfosztották a harmadik (inkomplett) pályáján (18 – 2 db) és a második (komplett) pályáján „keringő” elektronjaitól (8 db) és csak a belső pályáján lévő két elektront hagyták meg. Erről mondják azt, hogy hélium-szerűvé redukálták. Hát persze, mert a héliumnak csak két elektronja van. Viszont a héliumban csak két proton van (+ két neutron), de a vas atommagban nyüzsögnek a protonok és a neutronok. persze, hogy kurvára ion, pontosan 24 töltéssel. Most azt találták, hogy ezeknél a lecsupaszított atommagok körül „keringő” elektronok gerjesztésénél nem pont olyan hullámhosszú fotont találtak, mint „illet” volna. NEM MEGLEPŐ! Extrém körülmények között semmi se működik szabályosan. Majd meg fogják találni az okokat. Az elektromágneses erő él és virul, ahogy ezt 13,7 milliárd év óta teszi. Valaki írt egy szenzációs cikket az érdeklődő laikusoknak, amit valaki lefordított magyarra (a pasi jobban ért a két nyelvhez, mint a diszciplínához), hogy itt is szenzáció legyen azok között, akik 20 évvel később jöttek rá, hogy annak idején tanulni kellett volna.
6: Elismerem, nem vagyok otthon a témában, nekem sok mindent eladhatnak.
„Most azt találták, hogy ezeknél a lecsupaszított atommagok körül “keringő” elektronok gerjesztésénél nem pont olyan hullámhosszú fotont találtak, mint “illet” volna. NEM MEGLEPŐ! Extrém körülmények között semmi se működik szabályosan. ”
Azt írják, hogy nem az elmélet szerint viselkedik.
„Az NIST csapata azt vette észre, hogy az erős pozitív töltésű ionokban a fennmaradó elektronok észlelhetően más színű fotonokat generálnak, mint amit a QED megjósol.”
3. melike: Meg ne sértődj, de a gyermekednek mi az álma?
8!
Tudtam hogy megkérdezi valaki…Hát nem az az álma hogy vigye majd a munkát kenyeret táblát,és ehhez tenni is kell azért valamicskét..Természetesen nem sértődök meg..Hál Istennek ugyanaz az álma mint nekem,(óvodás kora óta errefelé terelem)de ő még csak a pénzt látja benne,hogy ebbe mennyi munka van azt még nem nagyon látja..Félek ha rájön hogy ez nem egyszerű dolog,elmegy a kedve.. 🙂 Mert szokott már játékokat irogatni,meg saját böngészőt,sőt saját operációs rendszerrel is készül már..Egy pár komolyabb játékkonzol is bánta már a próbálkozását elektronikailag,(ami nem kis pénz volt)
de itt vagyok mellette és együtt végig csináljuk..Azért vagyok..
Elnézést az offért..
7:
Értettem már az előbb is. Elolvastam az eredeti cikket is. Teljesen korrektül válaszoltam. Gondolj bele! Egy vasatomnak a 26 elektronjából leszakítanak 24-et. Extrém helyzet. 24 proton kifelé kurva nagy töltést ad. Ilyen körülmények között engem nem lep meg, hogy a két elektronhéj közötti energia különbség eltorzul. majd megtalálják a pontos okot, de az alaptörvény nem sérült. Viszont ad alkalmat egy kis szenzációra.
10. Egyetértek, a valóság nem mindig az aminek látszik!
Remek poszt.Ezért tartjuk Tibor bá’-t hogy az ilyesmit kimazsolázza nekünk 🙂 .Remélem egyébként hogy a tel-avivi fizikus téved.Kell egy kis titokzatosság.Ne tudjunk mindent megmérni! Kissé bosszantó lenne hogy rengeteg tudással felvértezve is kinyiffanunk mint civilizáció.
12:
Ami azt illeti elég sovány kenyéren tartotok. 😀
Azért nem kell az ilyen felfedezésektől nagyon magasra ugrani. A helyzet az, hogy a fizikában soha nem volt olyan elmélet, ami 100%-ig képes lett volna leírni a valóságot (Vagy akár annak egy megfigyelt részét) és soha nem is lesz (persze ez már világnézeti kérdés, amíg az ellenkezője be nem bizonyosodik).
Most éppen sikerült olyan kísérleti körülményeket teremteni, amelyekben nem látszik működni a szuperpozíció elve, illetve ezen a nyomon haladva talán még a Heisenberg-féle határozatlansági reláció is kétségbe vonható (ha jól értem). Vagyis 100 év után most éppen a kvantummechanikáról fog bebizonyosodni, hogy bizonyos körülmények között az alapelvei nem állják meg a helyüket. Pont, mint a relativitáselmélettel 1965-ben. Egy újabb fizikai elméletnek „járt le a szavatossága”. Ez van.
Ettől függetlenül ezeket még nem kell a kukába kidobni. A Newton-féle gravitációs törvényről is bebizonyosodott, hogy nem minden gravitációval kapcsolatos jelenség esetében ad pontos eredményeket, van azóta már legalább 2-3 újabb gravitációs elmélet is, ettől függetlenül Newton egyenleteivel számolva rengeteg hasznos dolgot lehet csinálni. A kvantummechanikának köszönhetünk olyan felfedezéseket, mint pl. a lézer vagy a számítógép, tehát korántsem haszontalan elmélet, csak lehet, hogy kénytelenek leszünk kidolgozni valami mást helyette bizonyos jelenségek vizsgálatához. Aztán az is lehet, hogy egy ilyen elmélet kidolgozása már meghaladja majd az elméleti fizikusok teljesítőképességét. Mert erre is volt már példa ám.
14.
„Pont, mint a relativitáselmélettel 1965-ben. Egy újabb fizikai elméletnek “járt le a szavatossága”. Ez van.”
Mi tortent 1965-ben? Nem tudtam rola, hogy az altrelnek lejart volna a „szavatossaga”.
15: Guzzi:
Az ált. rel. egy érdekes kérdés, de pl. a posztban is említett „quantum entanglement” gyakorlatilag ellentmond a spec. rel.-nek, hiszen amikor az egyik részecske állapotát megméred, akkor a tőle már adott esetben hatalmas távolságra lévő részecske állapota is eldől, méghozzá azonnal, vagyis a két részecske között a fénynél gyorsabban terjedő kapcsolat van.
1965 úgy jön ide (de most lehet, hogy nem pontosan emlékszem erre, guglival meg most nem tudtam neked erre rátalálni), hogy ha jól emlékszem, Einstein még a halála előtt felvetett egy gondolatkísérletet, ami tulajdonképpen pontosan a fent leírt problémát boncolgatta, majd 1965-ben sikerült először egy kísérletben is bizonyítani, hogy a quantum entanglement létezik, és bizony, a két részecske közötti kapcsolat gyorsabban terjed, mint a fény sebessége. Később azt is sikerült igazolni, hogy a részecskék állapota (spinje pl.) a mérés pillanatáig nem eldöntött.
Az ált. rel.-hez annyit: ha a spec. rel-lel problémák vannak, akkor bizony az ált. rel.-t is újra kell gondolnunk, hiszen a két elmélet szorosan összefügg. Egyébként még egyszer hangsúlyozom: soha nem volt még fizikai elmélet, amire ne lehetett volna kísérleti cáfolatot csinálni, és szerintem soha nem is lesz.
Asszem az EPR paradoxonra gondolsz (Einstein, Podolsky, Rosen). A specrel meg egyaltalan nem serul mivel ezzel a modszerrel (quantum entanglement) nem lehet informaciot kuldeni a fenynel gyorsabban. Hiaba tudod meg a masik reszecske allapotat azonnal, informaciot igy nem lehet kuldeni.
Gondold at. Semmilyen modon nem fogsz tudni informaciot kuldeni a fenynel gyorsabban. Az, hogy a tavoli reszecske allapotat azonnal megtudod ahogy a kozelit megmered, csak az informacio egyik fele. A masik fele az volt, hogy a reszecskeket osszefonodott allapotba hoztad. Ez pedig akkor tortent amikor meg egyutt voltak, onnantol mindket reszecske max fenysebesseggel haladt, vegul a meresnel megtudod az eredmenyt.
Ha nem tudod, hogy a reszecskek osszefonodottak-e akkor merhetsz akarmit, a masikrol nem tudsz semmit. Remelem vilagos volt.
17. Guzzi
Ha a két kommunikáló fél között félúton van egy „átjátszóállomás”, ami összefonódott részecskéket bocsát ki célzottan feléjük, akkor hiába a késleltetés a részecskék kibocsátásához képest, az információ teleportálódik. A kérdés inkább az, hogy az információ véletlenszerű, vagy meghatározhatjuk az egyik részecske állapotát? Ha egy polárszűrő-szerű alkalmatossággal egy bináris kódot megadhatunk a részecskék egyik felének, akkor a velük összefonódott párjukból kiolvashatjuk az infót.
A világegyetemben létező tömegvonzás jelensége hatásmechanizmusát tekintve hasonlónak fogható fel?Mármint, hogy a tömegek közötti
kölcsönhatás terjedési sebessége elméletileg akár a fénysebességet is meghaladhatja?Laikusként kérdezem.
19. Sztahi
A relativitáselmélet szerint a fény sebességével terjed a gravitációs erő. A mérési eredmények is ezt sugallják.
http://www.origo.hu/tudomany/vilagur/20030109alapveto.html
Szerintem egyszerűbb lett volna a kölcsönhatásmentes mérésről értekezni, ahhoz egy interferométer is elegendő, s ugyanide lehetett volna eljutni. További érdekesség, hogy ebben a cikkben
( http://www.complex.elte.hu/~geszti/ifm/ifm.ps.gz ) a szerző a kvantummechanikai szóráselmélet optikai tételéből kiindulva, előreszórással magyarázza a detektoroknál tapasztaltakat.